-
Let \(f(x)=x\) be a periodic function with period \(2\pi\).
-
Plot the graph of \(f(x)\) on the interval \(-3\pi\leq x\leq 3\pi\).
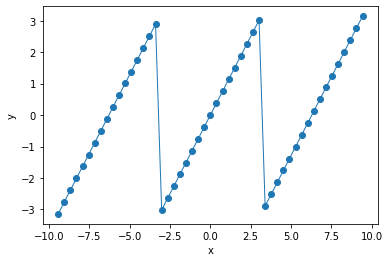
-
Find the Fourier series of \(f(x)\) on the interval \(-\pi
< x\leq \pi\)
Solution:
The function \(f(x) = x\) is odd on the interval \( (-\pi, \pi]\). Hence the Fourier series for \( f(x)\) has the simple form
\[ f(x) = \sum_{n=1}^\infty b_n \sin(n x)\]where the \(b_n\) are calculated using integration by parts:
\[\begin{align*} b_n &= \frac{2}{\pi}\int_{0}^\pi x \sin(nx)\,dx \\ & = -\frac{2}{\pi}\frac{x\cos(nx)}{n}\bigg\vert_0^\pi +\frac{2}{\pi n}\int_0^\pi \cos(n x)\, dx \\ & = -\frac{2}{\pi}\frac{\pi\cos(n\pi)}{n} + \cancel{\frac{2}{\pi n} \frac{\sin(nx)}{n}\bigg\vert_0^\pi} \\ & = \frac{2}{n}(-1)^{n+1} \end{align*} \]where we have used \(\cos(n\pi) = (-1)^n\). Therefore,
\[ f(x) = \sum_{n=1}^\infty \frac{2}{n}(-1)^{n+1}\sin(nx) \] -
State Parseval's identity for the Fourier coefficients derived in Part (b).
Solution:
Parseval's identity states that if \(f(x)\) has a Fourier series
\[ f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty \left( a_n \cos(nx) + b_n \sin(nx) \right)\]then
\[\frac{a_0^2}{2} + \sum_{n=1}^\infty\left(a_n^2 +b_n^2\right) = \frac{1}{\pi}\int_{-\pi}^{\pi} (f(x))^2\,dx\]Since \(a_0,a_n = 0\) for every \(n = 0,1,2,3,\cdots\) we have
\[ \frac{1}{\pi}\int_{-\pi}^\pi (f(x))^2\,dx = \sum_{n=1}^\infty b_n^2\]so in particular
\[ \frac{1}{\pi}\int_{-\pi}^\pi x^2\,dx= \sum_{n=1}^\infty \frac{4}{n^2} \] -
Use Parseval's identity stated in Part (c) to show that
\[ \frac{\pi^2}{6} = \displaystyle\sum_{n=1}^\infty\frac{1}{n^2} \]Solution:
\[\frac{1}{\pi}\int_{-\pi}^\pi x^2\,dx = \frac{2}{\pi}\int_0^\pi x^2\,dx = \frac{2}{3}\pi^2 \]By Parseval's identity, we obtain
\[\frac{2}{3}\pi^2 = \sum_{n=1}^\infty \frac{4}{n^2} \]which simplifies to
\[\frac{\pi^2}{6} = \sum_{n=1}^\infty \frac{1}{n^2}\] -
Suppose that \(f(x)\) is a periodic function on \([-L,L]\) satisfying
$$\int_{-L}^{L} (f(x))^2\,dx < \infty.$$
- Prove that for every \(n=0,1,2,3,\cdots\), we have
$$ \frac{a^2_0}{2} + \sum_{m=1}^n\left(a_m^2 + b_m^2\right)\leq \frac{1}{L}\int_{-L}^{L}(f(x))^2\,dx$$Hint: Consider the partial sum$$ S_n(x)=\frac{a_0}{2}+\sum_{m=1}^n\left[a_m\cos\left(\frac{m\pi}{L}x\right) + b_m\sin\left(\frac{m\pi}{L}x\right)\right]$$and expand the error term as$$\int_{-L}^{L}\left(f(x)-S_n(x)\right)^2\,dx $$
Solution:
\[\begin{align*} \int_{-L}^{L} \left(f(x) - S_n(x)\right)^2\,dx &=\int_{-L}^L (f(x))^2\,dx -2\int_{-L}^L f(x)S_n(x)\,dx + \int_{-L}^L (S_n(x))^2\,dx \end{align*} \]
Expanding the middle term, we get
\[\int_{-L}^L f(x)S_n(x)\,dx = \int_{-L}^L f(x)\left( \frac{a_0}{2}+\sum_{m=1}^n\left[a_m\cos\left(\frac{m\pi}{L}x\right) + b_m\sin\left(\frac{m\pi}{L}x\right)\right] \right)\,dx \]
Using the definition of \(a_0\), the first term above yields
\[\frac{a_0}{2}\int_{-L}^L f(x)\,dx = L {a_0^2}. \]
The second term above gives, after interchanging the integral and the sum and using the definition of \(a_m\)
\[\sum_{m=1}^n a_m\int_{-L}^L f(x)\cos\left(\frac{m\pi}{L}x\right)\, dx = La_m^2\]
Similarly, the last sum gives
\[\sum_{m=1}^n b_m\int_{-L}^L f(x)\sin\left(\frac{m\pi}{L}x\right)\, dx = Lb_m^2\]
Therefore,
\[\int_{-L}^L f(x)S_n(x)\,dx = L\left(\frac{a^2_0}{2}+\sum_{m=1}^n[a_m^2+b_m^2] \right) \].
Now consider the expansion of \(S^2_n(x)\). Due to the orthogonality of the Fourier series basis functions, we get
\[\int_{-L}^L S^2_n(x)\,dx = \int_{-L}^L \frac{a^2_0}{4}\,dx + \sum_{m=1}^n\int_{-L}^L \left[a_m^2\cos^2 \left(\frac{m\pi}{L}x\right) + b_m^2\sin^2 \left(\frac{m\pi}{L}x\right)\right]\,dx\]
Using the trig identities
\[\cos^2 (x) = \frac{1}{2}[1+\cos(2x)]\] \[\sin^2(x) = \frac{1}{2}[1-\cos(2x)]\]
we obtain finally
\[ \int_{-L}^L S^2_n(x) dx = L\left(\frac{a_0}{2} +\sum_{m=1}^n [a_m^2 + b_m^2]\right) \]
This shows that
\[\int_{-L}^L f(x)S_n(x)\,dx = \int_{-L}^L S^2_n(x)\, dx\]
Hence,
\[\int_{-L}^L \left(f(x) - S_n^2(x)\right)^2\,dx = \int_{-L}^L (f(x))^2\,dx - L\left(\frac{a_0}{2} +\sum_{m=1}^n [a_m^2 + b_m^2]\right) \]
The right hand side is an integral of a positive function, which is positive. Therefore
\[ L\left(\frac{a_0}{2} +\sum_{m=1}^n [a_m^2 + b_m^2]\right) \leq \frac{1}{L}\int_{-L}^L (f(x))^2\,dx. \]
-
Plot the graph of \(f(x)\) on the interval \(-3\pi\leq x\leq 3\pi\).
-
-
Compute the Fourier Transform of the function
$$f(x)=\begin{cases} 1, & \text{if } |x|\leq 1\\ 0, & \text{if } |x| > 1. \end{cases} $$
Solution:
The Fourier Transform of a function \(f(x)\) is given by
$$\widehat{f}(\mu) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty f(x)e^{i\mu x}\,dx $$
In this case, we have
$$\begin{align*} \widehat{f}(\mu) &= \frac{1}{\sqrt{2\pi}}\int_{-1}^1 e^{i\mu x}\,dx \\ & = \frac{1}{\sqrt{2\pi}}\int_{-1}^0 e^{i\mu x}\, dx + \frac{1}{\sqrt{2\pi}}\int_0^1 e^{i\mu x}\, dx \\ & = \frac{1}{\sqrt{2\pi}}\int_{0}^1 \left( e^{-i\mu x} + e^{i\mu x}\right)\,dx \\ & = \frac{2}{\sqrt{2\pi}} \int_0^1 \cos(\mu x)\, dx \\ & = \sqrt{\frac{2}{\pi}}\frac{\sin(\mu x)}{\mu} \end{align*} $$
-
Use the method of Fourier Transforms to solve the heat equation below, leaving your solution without the imaginary unit \(i\).
\[ \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2},\,\,\,-\infty < x < \infty,\,\,t> 0\]\[ u(x,0) = f(x) = \begin{cases}1, & \text{if } |x|\leq 1\\ 0, & \text{if } |x| > 1. \end{cases}\]
-
Compute the Fourier sine and cosine transforms of the functions below.
- \[f(x) = e^{-ax},\,\,\,a > 0\]
- \[ f(x) = \begin{cases}1, & \text{if } |x|\leq 1\\ 0, & \text{if } |x| > 1. \end{cases}\]
-
Use a Fourier sine transform to solve the heat equation
\[ \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2},\,\,\,0 < x < \infty,\,\,t> 0\]\[ u(x,0) = f(x) = e^{-x},\]\[u(0,t)=0. \]
-
Compute the Fourier Transform of the function